第十五讲:子空间投影
第十五讲:子空间投影
从$\mathbb{R}^2$空间讲起,有向量$a, b$,做$b$在$a$上的投影$p$,如图:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
plt.style.use("seaborn-dark-palette")
fig = plt.figure()
plt.axis('equal')
plt.axis([-7, 7, -6, 6])
plt.arrow(-4, -1, 8, 2, head_width=0.3, head_length=0.5, color='r', length_includes_head=True)
plt.arrow(0, 0, 2, 4, head_width=0.3, head_length=0.5, color='b', length_includes_head=True)
plt.arrow(0, 0, 48/17, 12/17, head_width=0.3, head_length=0.5, color='gray', length_includes_head=True)
plt.arrow(48/17, 12/17, 2-48/17, 4-12/17, head_width=0.3, head_length=0.5, color='g', length_includes_head=True)
# plt.plot([48/17], [12/17], 'o')
# y=1/4x
# y=-4x+12
# x=48/17
# y=12/17
plt.annotate('b', xy=(1, 2), xytext=(-30, 15), textcoords='offset points', size=20, arrowprops=dict(arrowstyle="->"))
plt.annotate('a', xy=(-1, -0.25), xytext=(15, -30), textcoords='offset points', size=20, arrowprops=dict(arrowstyle="->"))
plt.annotate('e=b-p', xy=(2.5, 2), xytext=(30, 0), textcoords='offset points', size=20, arrowprops=dict(arrowstyle="->"))
plt.annotate('p=xa', xy=(2, 0.5), xytext=(-20, -40), textcoords='offset points', size=20, arrowprops=dict(arrowstyle="->"))
plt.grid()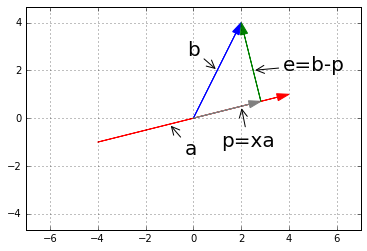
plt.close(fig)从图中我们知道,向量$e$就像是向量$b, p$之间的误差,$e=b-p, e \bot p$。$p$在$a$上,有$\underline{p=ax}$。
所以有$a^Te=a^T(b-p)=a^T(b-ax)=0$。关于正交的最重要的方程:
$$
a^T(b-xa)=0 \
\underline{xa^Ta=a^Tb} \
\underline{x=\frac{a^Tb}{a^Ta}} \
p=a\frac{a^Tb}{a^Ta}
$$
从上面的式子可以看出,如果将$b$变为$2b$则$p$也会翻倍,如果将$a$变为$2a$则$p$不变。
设投影矩阵为$P$,则可以说投影矩阵作用与某个向量后,得到其投影向量,$projection_p=Pb$。
易看出$\underline{P=\frac{aa^T}{a^Ta}}$,若$a$是$n$维列向量,则$P$是一个$n \times n$矩阵。
观察投影矩阵$P$的列空间,$C(P)$是一条通过$a$的直线,而$rank(P)=1$(一列乘以一行:$aa^T$,而这一列向量$a$是该矩阵的基)。
投影矩阵的性质:
- $\underline{P=P^T}$,投影矩阵是一个对称矩阵。
- 如果对一个向量做两次投影,即$PPb$,则其结果仍然与$Pb$相同,也就是$\underline{P^2=P}$。
为什么我们需要投影?因为就像上一讲中提到的,有些时候$Ax=b$无解,我们只能求出最接近的那个解。
$Ax$总是在$A$的列空间中,而$b$却不一定,这是问题所在,所以我们可以将$b$变为$A$的列空间中最接近的那个向量,即将无解的$Ax=b$变为求有解的$A\hat{x}=p$($p$是$b$在$A$的列空间中的投影,$\hat{x}$不再是那个不存在的$x$,而是最接近的解)。
现在来看$\mathbb{R}^3$中的情形,将向量$b$投影在平面$A$上。同样的,$p$是向量$b$在平面$A$上的投影,$e$是垂直于平面$A$的向量,即$b$在平面$A$法方向的分量。
设平面$A$的一组基为$a_1, a_2$,则投影向量$p=\hat{x_1}a_1+\hat{x_2}a_2$,我们更倾向于写作$p=A\hat{x}$,这里如果我们求出$\hat{x}$,则该解就是无解方程组最近似的解。
现在问题的关键在于找$e=b-A\hat{x}$,使它垂直于平面,因此我们得到两个方程
$
\begin{cases}a_1^T(b-A\hat{x})=0\
a_2^T(b-A\hat{x})=0\end{cases}
$,将方程组写成矩阵形式
$
\begin{bmatrix}a_1^T\a_2^T\end{bmatrix}
(b-A\hat{x})=
\begin{bmatrix}0\0\end{bmatrix}
$,即$A^T(b-A\hat{x})=0$。
比较该方程与$\mathbb{R}^2$中的投影方程,发现只是向量$a$变为矩阵$A$而已,本质上就是$A^Te=0$。所以,$e$在$A^T$的零空间中($e\in N(A^T)$),从前面几讲我们知道,左零空间$\bot$列空间,则有$e\bot C(A)$,与我们设想的一致。
再化简方程得$A^TAx=A^Tb$,比较在$\mathbb{R}^2$中的情形,$a^Ta$是一个数字而$A^TA$是一个$n$阶方阵,而解出的$x$可以看做两个数字的比值。现在在$\mathbb{R}^3$中,我们需要再次考虑:什么是$\hat{x}$?投影是什么?投影矩阵又是什么?
- 第一个问题:$\hat x=(A^TA)^{-1}A^Tb$;
- 第二个问题:$p=A\hat x=\underline{A(A^TA)^{-1}A^T}b$,回忆在$\mathbb{R}^2$中的情形,下划线部分就是原来的$\frac{aa^T}{a^Ta}$;
- 第三个问题:易看出投影矩阵就是下划线部分$P=A(A^TA)^{-1}A^T$。
这里还需要注意一个问题,$P=A(A^TA)^{-1}A^T$是不能继续化简为$P=AA^{-1}(A^T)^{-1}A^T=I$的,因为这里的$A$并不是一个可逆方阵。
也可以换一种思路,如果$A$是一个$n$阶可逆方阵,则$A$的列空间是整个$\mathbb{R}^n$空间,于是$b$在$\mathbb{R}^n$上的投影矩阵确实变为了$I$,因为$b$已经在空间中了,其投影不再改变。
再来看投影矩阵$P$的性质:
- $P=P^T$:有
$
\left[A(A^TA)^{-1}A^T\right]^T=A\left[(A^TA)^{-1}\right]^TA^T
$,而$(A^TA)$是对称的,所以其逆也是对称的,所以有$A((A^TA)^{-1})^TA^T=A(A^TA)^{-1}A^T$,得证。 - $P^2=P$:有
$
\left[A(A^TA)^{-1}A^T\right]\left[A(A^TA)^{-1}A^T\right]=A(A^TA)^{-1}\left[(A^TA)(A^TA)^{-1}\right]A^T=A(A^TA)^{-1}A^T
$,得证。
最小二乘法
接下看看投影的经典应用案例:最小二乘法拟合直线(least squares fitting by a line)。
我们需要找到距离图中三个点 $(1, 1), (2, 2), (3, 2)$ 偏差最小的直线:$b=C+Dt$。
plt.style.use("seaborn-dark-palette")
fig = plt.figure()
plt.axis('equal')
plt.axis([-1, 4, -1, 3])
plt.axhline(y=0, c='black', lw='2')
plt.axvline(x=0, c='black', lw='2')
plt.plot(1, 1, 'o', c='r')
plt.plot(2, 2, 'o', c='r')
plt.plot(3, 2, 'o', c='r')
plt.annotate('(1, 1)', xy=(1, 1), xytext=(-40, 20), textcoords='offset points', size=14, arrowprops=dict(arrowstyle="->"))
plt.annotate('(2, 2)', xy=(2, 2), xytext=(-60, -5), textcoords='offset points', size=14, arrowprops=dict(arrowstyle="->"))
plt.annotate('(3, 2)', xy=(3, 2), xytext=(-18, 20), textcoords='offset points', size=14, arrowprops=dict(arrowstyle="->"))
plt.grid()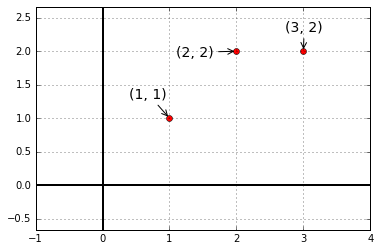
plt.close(fig)根据条件可以得到方程组
$
\begin{cases}
C+D&=1 \
C+2D&=2 \
C+3D&=2 \
\end{cases}
$,写作矩阵形式
$\begin{bmatrix}1&1 \1&2 \1&3\\end{bmatrix}\begin{bmatrix}C\D\\end{bmatrix}=\begin{bmatrix}1\2\2\\end{bmatrix}$,也就是我们的$Ax=b$,很明显方程组无解。但是$A^TA\hat x=A^Tb$有解,于是我们将原是两边同时乘以$A^T$后得到的新方程组是有解的,$A^TA\hat x=A^Tb$也是最小二乘法的核心方程。
下一讲将进行最小二乘法的验算。
